图算法系列之深度优先搜索(二)
在上篇中我们学习了深度优先搜索,知道了如何通过深度优先搜索在图中寻找路径;本篇我们继续一起来学习深度优先搜索算法的其他应用场景
连通分量
从一幅图中找出所有的连通分量,这是也是深度优先搜索的一个应用场景。什么是连通分量?这个定义在之前的文章中已有提到《如何检测社交网络中两个人是否是朋友关系(union-find算法)》
在这篇采用的是union-find算法实现的连通性检查,本篇我们将采用深度优先搜索的方式来找出图中的所有连通分量
连通分量的API定义
public class DepthFirstCC {
public DepthFirstCC(Graph graph);
public boolean connected(int v, int w); //检查两个顶点是否连通
public int count(); //统计连通分量的总数
public int id(int v); //顶点v所在连通分量的标识
}连通分量的API实现
与之前一样没扫描到一个顶点我们就需要标记这个顶点,所以依然需要定义一个marked[]数组
为了统计出图中总共有多少连通分量,所以需要定义一个变量count
为了判断两个顶点是否相连,我们需要把相连的顶点对应的标识值记录成相同值,当在调用connected方法的时候直接取出两个顶点的标识值比较,如果相同就是连通的,否则就是非连通;
这个的标识值我们使用的是count的值,每个顶点都需要存一个标识值,所以还需要一个ids[]数组。
public class DepthFirstCC {
private boolean marked[];
private int count;
private int[] ids;
public DepthFirstCC(Graph graph) {
this.marked = new boolean[graph.V()];
this.ids = new int[graph.V()];
for (int v = 0; v < graph.V(); v++) {
if (!this.marked[v]) {
dfs(graph, v);
count++;
}
}
}
private void dfs(Graph graph, int v) {
this.marked[v] = true;
this.ids[v] = count;
for (int w : graph.adj(v)) {
if (!this.marked[w]) {
dfs(graph, w);
}
}
}
public boolean connected(int v, int w) {
return id(v) == id(w);
}
public int count() {
return count;
}
public int id(int v) {
return ids[v];
}
}单元测试
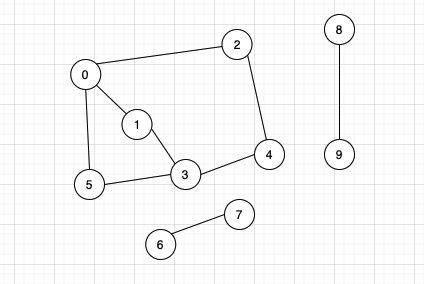
构造这样一个图,连通分量的总数应该是3
@Test
public void test() {
Graph graph = new Graph(10);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(0, 5);
graph.addEdge(1, 3);
graph.addEdge(2, 4);
graph.addEdge(4, 3);
graph.addEdge(5, 3);
graph.addEdge(6, 7);
graph.addEdge(8, 9);
DepthFirstCC cc = new DepthFirstCC(graph);
System.out.println(cc.connected(0,5));
System.out.println(cc.connected(1,2));
System.out.println(cc.count());
}基于深度优先搜索实现的连通性检查理论上说要比以前实现的union-find算法更快,因为检查连通性深度优先搜索实现的版本能够保证在常量时间内完成,而union-find算法不行;
但是union-find也有自己的优势: 不需要把完整的构造并表示一张图,更重要的是union-find算法是动态的添加节点。
检查无向图中是否有环
为了减小实现的复杂度,我们假设图中不存在自环和平行边;
假如从顶点v出发存在环,表示从顶点v出发的连通分量中某个顶点的邻接顶点是v,那么在搜索的过程中必定会再次遇到顶点v
实现的思路:
- 标记已经搜索过的每个顶点
- 当遇到了一个已经被标记过的顶点,表示已经图中存在环;
- 由于图是无向图,如果v-w相连,那么顶点v中的邻接表中有w,w邻接表中也会有v,但是他们没有构成环,所以需要排除掉该情况。
public class Cycle {
private boolean marked[];
private boolean hashCycle;
public Cycle(Graph graph) {
this.marked = new boolean[graph.V()];
for (int s = 0; s < graph.V(); s++) {
if (!this.marked[s]) {
dfs(graph, s, s);
}
}
}
private void dfs(Graph graph, int v, int pV) {
this.marked[v] = true;
for (int w : graph.adj(v)) {
if (!this.marked[w]) {
this.dfs(graph, w, v);
} else if (w != pV) {
this.hashCycle = true;
return;
}
}
}
public boolean hasCycle() {
return hashCycle;
}
}方法dfs的参数v表示需要待搜索的顶点,pV表示的是到达v的顶点,所以如果v的邻接表中有个顶点已被标记过并且该顶点不等于到达v的顶点,那么表示图中有环
检查无向图是否是二分图
何为二分图? 图中每条边所连接的顶点都属于不同的部分;如下图:
其中红色节点表示一个集合,白色节点是另一个集合,每条边连接的两个顶点属于不同的集合;
举个实际的例子就很好理解,电影与演员的关系,电影作为一个顶点,演员作为一个顶点,电影与电影直接是不会有边,演员与演员直接也不会有边,这就是一张二分图。
public class TwoColorGraph {
private boolean twoColor = true;
private boolean[] marked;
private boolean[] color;
public TwoColorGraph(Graph graph) {
this.marked = new boolean[graph.V()];
this.color = new boolean[graph.V()];
for (int v = 0; v < graph.V(); v++) {
if (!this.marked[v]) {
dfs(graph, v);
}
}
}
private void dfs(Graph graph, int v) {
this.marked[v] = true;
for (int w : graph.adj(v)) {
if (!this.marked[w]) {
this.color[w] = !this.color[v];
dfs(graph, w);
} else if (this.color[w] == this.color[v]) {
this.twoColor = false;
return;
}
}
}
public boolean isTwoColor() {
return twoColor;
}
}