图算法系列之深度优先搜索（一）

前言

在上一篇中我们把图通过邻接表数组表示出来了，这个数据结构将会做我们实现图算法的基础，本篇我们将一起开始学习图算法的第一个搜索算法 - 深度优先搜索

搜索API的定义

public class Search {
    Search(Graph graph, int s);

    boolean marked(int v);
    
    int count();
}

在开始实现算法之前，我们依然先来定义搜索的API

1. 构造方法提供了一个图对象，以及一个起点s，需要找到与s连通的所有顶点
2. marked判断顶点s与v是否相邻
3. count返回与顶点s相连的总顶点数

深度优先搜索

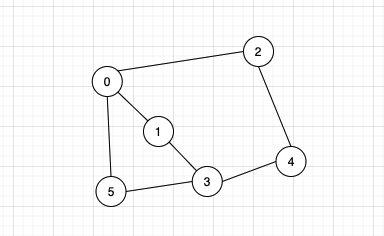
假如上图是一个迷宫，我们需要从顶点0开始找到一条出路，假设我们有一条无限长的绳子，和一支粉笔，那么可以这样考虑找到出路：

1. 先选择一条通道走，在走的路上放上一根绳子
2. 每遇到一个路口就用笔标记一下，继续选择一条未走过的通道
3. 当遇到一个已经被标记的路口时就退回到上一个路口继续选择一个未走过的通道
4. 当回退的路口已经没有路可以走的时候就在继续往后回退

这种方式绳子总能帮你找到一条出路，而标记不会让你重复走已经走过的通道。

深度优先搜索的实现思路就和走迷宫的方式一样；

public class DepthFirstSearch {
    private boolean marked[]; 
    private int count;

    public DepthFirstSearch(Graph graph, int s) {
        this.marked = new boolean[graph.V()];
        this.dfs(graph, s);
    }

    private void dfs(Graph graph, int v) {
        marked[v] = true;
        count++;
        for (int w : graph.adj(v)) {
            if (!marked[w]) {
                dfs(graph, w);
            }
        }
    }

    @Override
    public boolean marked(int v) {
        return marked[v];
    }

    @Override
    public int count() {
        return count;
    }
}

在搜索一张图的时候，使用递归来遍历所有的顶点，在访问其中一个顶点时：

1. 标记它被已经访问
2. 递归的访问与之相连的所有邻接点

单元测试： 构建下面这张图，然后测试深度优先搜索

@Test
public void test() {
    Graph graph = new Graph(8); //构建一张图
    graph.addEdge(0, 1);
    graph.addEdge(0, 2);
    graph.addEdge(0, 5);
    graph.addEdge(1, 3);
    graph.addEdge(2, 4);
    graph.addEdge(4, 3);
    graph.addEdge(5, 3);
    
    graph.addEdge(6, 7); //为了展示

    SeDepthFirstSearcharch search = new DepthFirstSearch(graph, 0);
    System.out.println(search.count());
    System.out.println(search.marked(6));
    System.out.println(search.marked(7));
    System.out.println(search.marked(2));
    System.out.println(search.marked(5));
}

寻找路径的API

以上的递归算法只是一个开始，从上面的结果我们可以看出，我们只能判断出哪些顶点与起点s是连通的，无法给出具体的路径出来；换句话说，我们需要实现从顶点s到顶点v是否存在路径可达，如果存在请打印出来

public class Paths {
    Paths(Graph graph, int s);
    
    boolean hasPathTo(int v); //判断出从s->v是否存在路径
    
    Iterable<Integer> pathTo(int v); //如果存在路径，返回路径
}

基于深度优先搜索查找图中的可达路径

我们依然基于这张图来看，由于我们需要找出可达的路径，所以我们在进行搜索的时候需要记录下图中的边，这里我们使用的是一个数组edgeTo[]，如果存在一条边是v->w，那么可以表示成edgeTo[w]=v，在深度搜索完成之后这个edgeTo[]数组就是一颗由父链表示的一颗树 （父链树在之前的文章中也使用过《如何检测社交网络中两个人是否是朋友关系（union-find算法）》）

public class DepthFirstPaths {
    private boolean marked[];
    private int[] edgeTo;
    private int s;

    DepthFirstPaths(Graph graph, int s) {
        this.s = s;
        this.marked = new boolean[graph.V()];
        this.edgeTo = new int[graph.V()];
        this.dfs(graph, s);
    }

    private void dfs(Graph graph, int v) {
        this.marked[v] = true;
        for (int w : graph.adj(v)) {
            if (!marked[w]) {
                this.edgeTo[w] = v;
                this.dfs(graph, w);
            }
        }
    }

    public boolean hasPathTo(int v) {
        return marked[v];
    }

    public Iterable<Integer> pathTo(int v) {
        if (!hasPathTo(v)) {
            throw new IllegalStateException("s不能到达v");
        }
        Stack<Integer> stack = new LinkedListStack<>();
        stack.push(v);
        while (edgeTo[v] != s) {
            stack.push(edgeTo[v]);
            v = edgeTo[v];
        }
        stack.push(s);
        return stack;
    }
}

画图来详细跟踪深度优先搜索的运行轨迹，记录了edgeTo的变化以及父链树的逐渐形成

最终父链树形成了，接下来我们来写单元测试校验下生成的父链树和实际的运行结果是否一致

@Test
public void test() {
    Graph graph = new Graph(8);
    graph.addEdge(0, 1);
    graph.addEdge(0, 2);
    graph.addEdge(0, 5);
    graph.addEdge(1, 3);
    graph.addEdge(2, 4);
    graph.addEdge(4, 3);
    graph.addEdge(5, 3);
    graph.addEdge(6, 7);

    DepthFirstPaths paths = new DepthFirstPaths(graph, 0);
    System.out.println(paths.hasPathTo(5));
    System.out.println(paths.hasPathTo(2));
    System.out.println(paths.hasPathTo(6));

    paths.pathTo(5).forEach(System.out::print);
    System.out.println();
    paths.pathTo(4).forEach(System.out::print);
    System.out.println();
    paths.pathTo(2).forEach(System.out::print);


}

验证结果完全匹配了父链树