如何检测社交网络中两个人是否是朋友关系

前言

春节放假会了老家，停更了很多天，这是年后连夜肝出来的第一篇文章，先来聊聊春节放假期间发生的事，这次回家遇到了我学生时代的女神，当年她在我心目中那是

"出淤泥而不染、濯清涟而不妖"

没想到这次回家遇到了她，身体发福了，心目中女神的形象瞬间碎了，就好像达芬奇再次遇到了蒙娜丽莎

"菡萏香销翠叶残"

好了，言归正传。

有时候我们可以需要判断在大型网络中两台计算机是否相连，是否需要建立一条新的连接才能通信；或者是在社交网络中判断两个人是否是朋友关系（相连表示是朋友关系）。在这种应用中，通常我们可能需要处理数百万的对象和数亿的连接，如何能够快速的判断出是否相连呢？这就需要使用到union-find算法

概念

相连

假如输入一对整数，其中每个数字表示的是某种对象（人、地址或者计算机等等），整数对p,q理解为“p与q相连”，相连具有以下特性：

• 自反性：p与p是相连的
• 对称性：如果p与q相连，那么q与p相连
• 传递性：如果p与q相连，q与r相连，那么p与r也相连

对象如何与数字关联起来，后面我们聊到一种算法符号表

等价类

假设相连是一个种等价关系，那么等价关系能够将对象划分为多个等价类，在该算法中，当且仅当两个对象相连时他们才属于同一个等价类

触点

整个网络中的某种对象称为触点

连通分量

将整数对称为连接，将等价类称作连通分量或者简称分量

动态连通性

union-find算法的目标是当程序从输入中读取了整数对p q时，如果已知的所有整数对都不能说明p q是相连的，那么将这一对整数输出，否则忽略掉这对整数；我们需要设计数据结构来保存已知的所有整数对的信息，判断出输入的整数对是否是相连的，这种问题叫做动态连通性问题。

union-find算法API定义

public interface UF {
    void union(int p, int q); //在p与q之间添加一条连接

    int find(int p); //返回p所在分量的标识符

    boolean connected(int p, int q); //判断出p与q是否存在于同一个分量中

    int count(); //统计出连通分量的数量
}

如果两个触点在不同的分量中，union操作会使两个分量归并。一开始我们有N个分量（每个触点表示一个分量），将两个分量归并之后数量减一。

抽象实现如下：

public abstract class AbstractUF implements UF {
    protected int[] id;
    protected int count;

    public AbstractUF(int N) {
        count = N;

        id = new int[N];
        for (int i = 0; i < N; i++) {
            id[i] = i;
        }
    }

    @Override
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }

    @Override
    public int count() {
        return count;
    }
}

接下来我们就主要来讨论如何实现union方法和find方法

quick-find算法

这种算法的实现思路是在同一个连通分量中所有触点在id[]中的值都是相同的，判断是否连通的connected的方法就是判断id[p]是否等于id[q]。

public class QuickFindImpl extends AbstractUF {
    public QuickFindImpl(int N) {
        super(N);
    }

    @Override
    public int find(int p) {
        return id[p];
    }

    @Override
    public void union(int p, int q) {
        int pId = find(p);
        int qId = find(q);

        if (pId == qId) { //如果相等表示p与q已经属于同一分量中
            return;
        }

        for (int i = 0; i < id.length; i++) {
            if (id[i] == pId) {
                id[i] = qId; //把分量中所有的值都统一成qId
            }
        }
        count--; //连通分量数减一
    }

}

• 算法分析： find()操作显然是很快的，时间复杂度O(1), 但是union的算法是无法处理大型数据的，因为每次都需要变量整个数组，那么union方法的时间复杂度是O(n)

quick-union算法

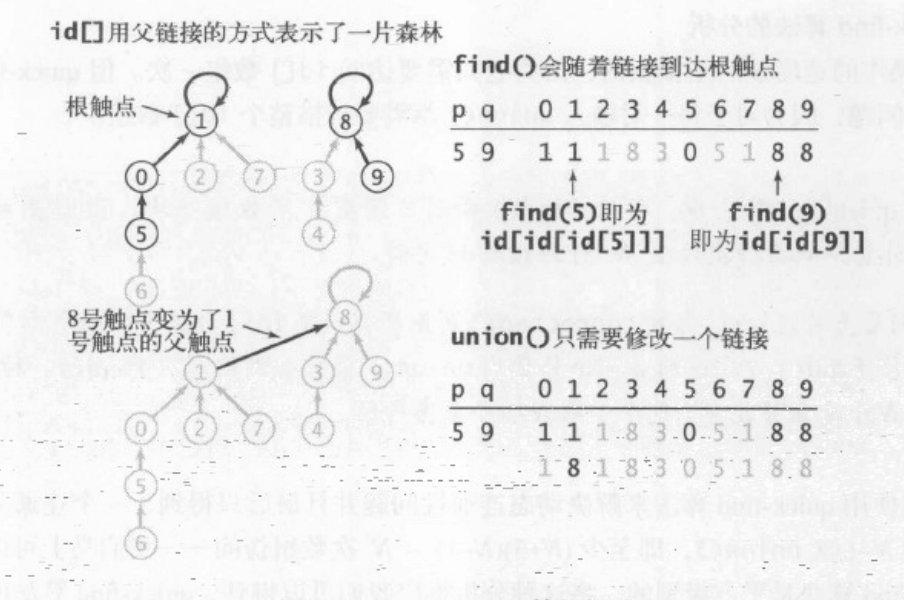
为了提高union方法的速度，我们需要考虑另外一种算法；使用同样的数据结构，只是重新定义id[]表示的意义，每个触点所对应的id[]值都是在同一分量中的另一个触点的名称

在数组初始化之后，每个节点的链接都指向自己；id[]数组用父链接的形式表示了森林，每一次union操作都会找出每个分量的根节点进行归并。

public class QuickUnionImpl extends AbstractUF {
    public QuickUnionImpl(int N) {
        super(N);
    }

    @Override
    public int find(int p) {
        //找出p所在分量的根触点
        while (p != id[p]) {
            p = id[p];
        }
        return p;
    }

    @Override
    public void union(int p, int q) {
        int pRoot = find(p); //找出q p的根触点
        int qRoot = find(q);
        if (pRoot == qRoot) { //处于同一分量不做处理
            return;
        }
        id[pRoot] = qRoot; //根节点
        count--;
    }

}

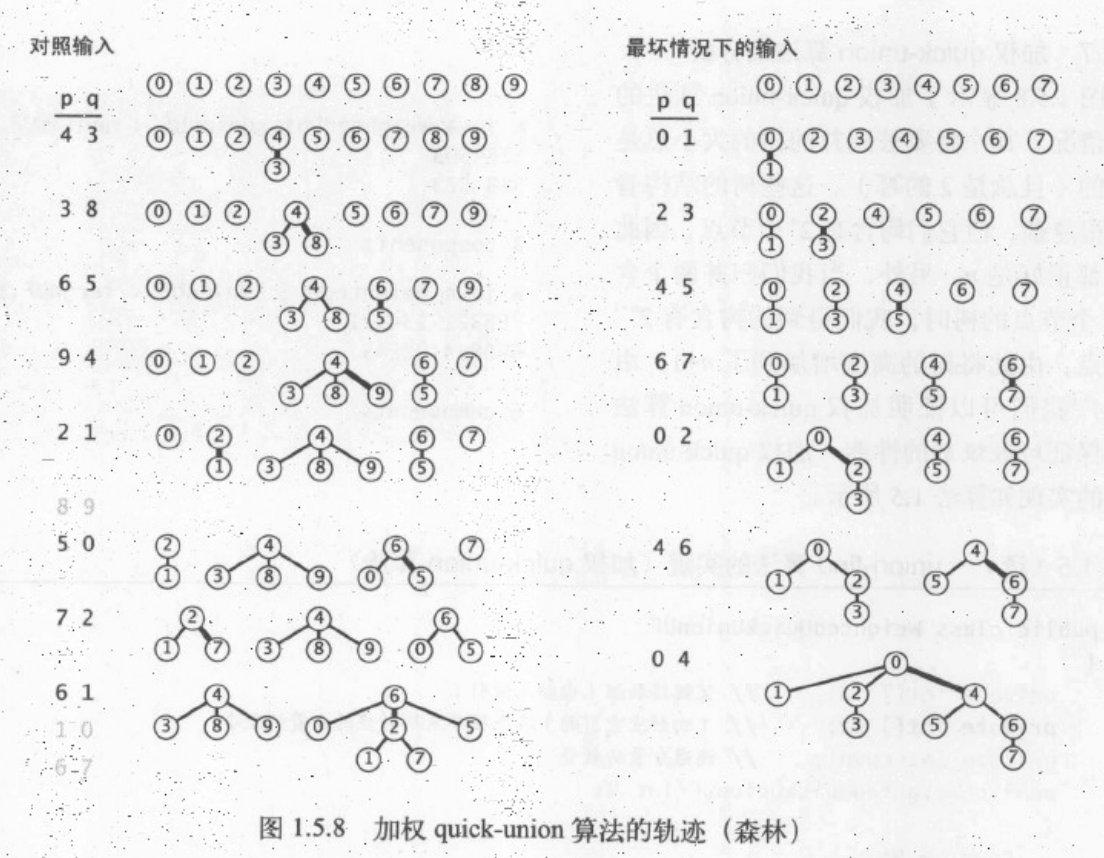
• 算法分析： 看起来quick-union算法比quick-find算法更快，因为union不需要为每对输入遍历整个数组， 考虑最佳情况下，find方法只需要访问一次数组就可以得到根触点，那么union方法的时间复杂度O(n)； 考虑到最糟糕的输入情况，如下图：

find方法需要访问数组n-1次，那么union方法的时间复杂度是O(n²)

加权quick-union算法

为了保证quick-union算法最糟糕的情况不在出现，我需要记录每一个树的大小，在进行分量归并操作时总是把小的树连接到大的树上，这种算法构造出来树的高度会远远小于未加权版本所构造的树高度。

public class WeightedQuickUnionImpl extends AbstractUF {
    private int[] sz;

    public WeightedQuickUnionImpl(int N) {
        super(N);
        sz = new int[N];
        for (int i = 0; i < N; i++) {
            sz[i] = 1;
        }
    }

    @Override
    public void union(int p, int q) {
        int pRoot = find(p); //找出q p的根触点
        int qRoot = find(q);
        if (pRoot == qRoot) { //处于同一分量不做处理
            return;
        }
        //小树合并到大树
        if (sz[pRoot] < sz[qRoot]) {
            sz[qRoot] += sz[pRoot]; 
            id[pRoot] = qRoot;
        } else {
            sz[pRoot] += sz[qRoot];
            id[qRoot] = pRoot;
        }
        count--;
    }

    @Override
    public int find(int p) {
        //找出p所在分量的根触点
        while (p != id[p]) {
            p = id[p];
        }
        return p;
    }
}

• 算法分析： 最坏的情况下，每次union归并的树都是大小相等的，他们都包含了2的n次方个节点，高度都是n，合并之后的高度变成了n+1，由此可以得出union方法的时间复杂度是O(lgN)

总结

union-find算法只能判断出给定的两个整数是否是相连的，无法给出具体达到的路径；后期我们聊到图算法可以给出具体的路径

算法	union()	find()
quick-find算法	N	1
quick-union算法	树的高度	树的高度
加权quick-union算法	lgN	lgN

---

参考书籍：算法第四版